
排序算法
选择排序
从头开始,以当前i的后一位为待排序元素,默认是最小元素 ,每次从未排序的序列里将选择最小的元素选择出来。
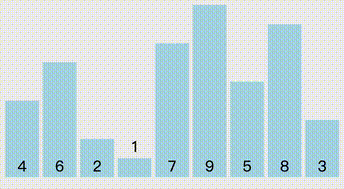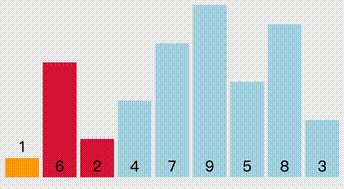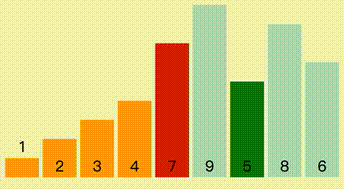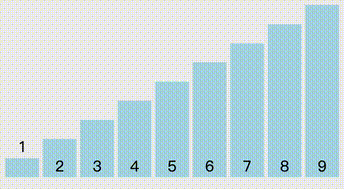
//选择排序 public static void SelectionSort(int[] arr) { Console.WriteLine("选择排序"); for (int i = 0; i < arr.Length - 1; i++) { int minIndex = i; for (int j = i + 1; j < arr.Length; j++) { if (arr[j] < arr[minIndex]) { minIndex = j; } } Swap(ref arr[i], ref arr[minIndex]); } }冒泡排序
从头开始,每轮比较也是从头开始,每次都是以临近两个元素之间交换,每轮比较的序列长度是length - i 个。
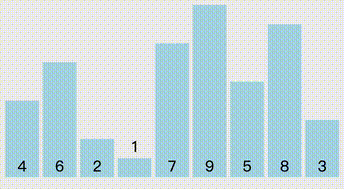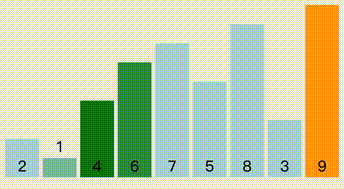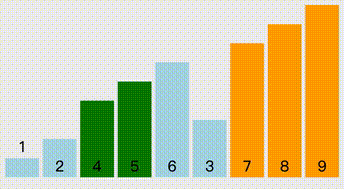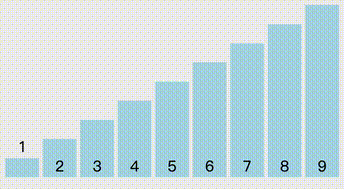
//冒泡排序public static void BubbleSort(int[] arr){ Console.WriteLine("冒泡排序"); for (int i = 0; i < arr.Length - 1; i++) { for (int j = 0; j < arr.Length - i - 1; j++) { if (arr[j] > arr[j + 1]) { Swap(ref arr[j], ref arr[j + 1]); } } }}插入排序
从头开始,每次读取已排好序列的下一位元素,通过不断比较上一位元素大小,不断向前插入,直到合适位置。
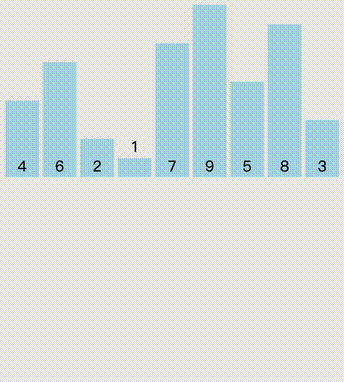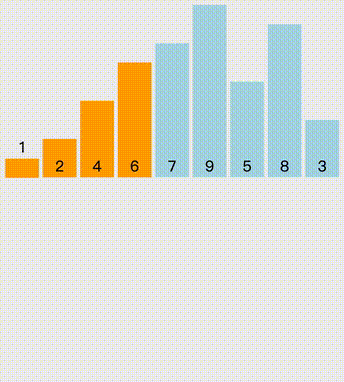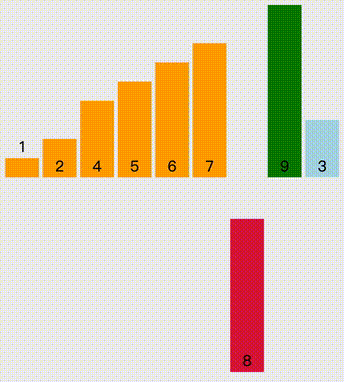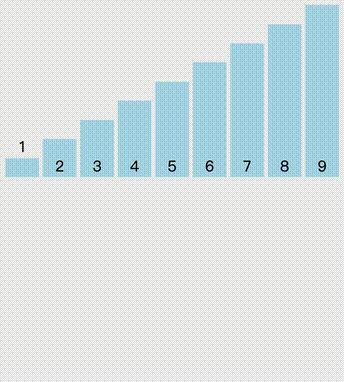
//插入排序public static void InsertionSort(int[] arr){ Console.WriteLine("插入排序"); for (int i = 1; i < arr.Length; i++) { int temp = arr[i]; int j = i - 1; while (j >= 0 && arr[j] > temp) { arr[j + 1] = arr[j]; j--; } arr[j + 1] = temp; }}希尔排序
希尔排序的本质是优化版的插入排序,先将序列分组,gap为总长度的一半,元素下标 % gap 数值相同的为一组,组内使用插入排序,排序之后继续分组继续排序,直到gap为1排序完成之后就是最终结果。

//希尔排序 public static void ShellSort(int[] arr) { Console.WriteLine("希尔排序"); // 初始化间隔值为数组长度的一半 int gap = arr.Length / 2;
// 当间隔大于0时持续分组排序 while (gap > 0) { // 从gap位置开始遍历数组 for (int i = gap; i < arr.Length; i++) { // 保存当前待插入元素 int temp = arr[i]; // 初始化比较位置(前一个间隔位置的索引) int j = i - gap; // 在子序列中进行插入排序 while (j >= 0 && arr[j] > temp) { // 将较大元素后移间隔位 arr[j + gap] = arr[j]; // 向前检查同子序列的元素 j -= gap; } // 插入元素到正确位置 arr[j + gap] = temp; } // 缩小间隔(常见缩减方式为折半) gap /= 2; } }归并排序
采用递归的思想,先分再和,通过递归拆解,直到无法继续拆解之后,比较两个子数组,选最小的元素放在新数组的前面,直到排序完成,再经过递归两两组合继续比较,直到所有排序完成。
计算顺序如下
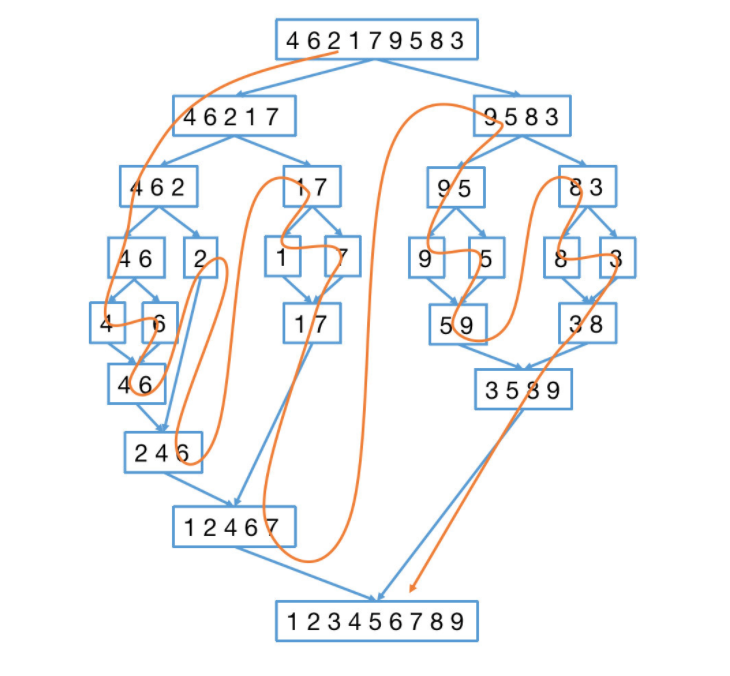
#region 归并排序 //归并排序 // 归并排序入口方法 public static void MergeSort(int[] arr) { //Console.WriteLine("归并排序"); if (arr == null || arr.Length < 2) return; // 边界条件检查
// 调用递归排序方法,传入数组和边界索引 Sort(arr, 0, arr.Length - 1); }
// 递归分解方法 private static void Sort(int[] arr, int left, int right) { //Console.WriteLine("拆分阶段left:"+left+","+"right:"+right); // 递归终止条件 if (left >= right) { //Console.WriteLine("数组长度小于2,无法拆分"); return; }
// 计算中间点(防止整数溢出) int mid = left + (right - left) / 2;
// 递归排序左半部分 Sort(arr, left, mid); // 递归排序右半部分 Sort(arr, mid + 1, right);
// 合并两个有序部分 Merge(arr, left, mid, right); }
// 合并两个有序子数组 private static void Merge(int[] arr, int left, int mid, int right) { //Console.WriteLine("合并阶段left:"+left+","+"right:"+right); // 创建临时数组存放合并结果 int[] temp = new int[right - left + 1];
int i = left; // 左子数组起始索引 int j = mid + 1; // 右子数组起始索引 int k = 0; // 临时数组索引
// 合并两个子数组 while (i <= mid && j <= right) { // 比较两个子数组当前元素,取较小者 temp[k++] = arr[i] <= arr[j] ? arr[i++] : arr[j++]; }
// 处理剩余元素(只会有一个子数组有剩余) while (i <= mid) temp[k++] = arr[i++]; while (j <= right) temp[k++] = arr[j++];
// 将排序结果复制回原数组 Array.Copy(temp, 0, arr, left, temp.Length); for (int a = 0; a < temp.Length; a++) { Console.Write(temp[a]+" "); } Console.WriteLine(); } #endregion测试数据 int[] testData = [54, 23, 32, 86, 75, 3, 212, 443, 31, 97 , 100];排序顺序打印结果23 5423 32 5475 863 75 863 23 32 54 75 86212 44331 212 44397 10031 97 100 212 4433 23 31 32 54 75 86 97 100 212 443数据量:11 条排序耗时:4 毫秒
测试数据 int[] testData = [54, 23, 32, 86, 75, 3, 212, 443, 31, 97];排序顺序打印结果23 5423 32 5475 8623 32 54 75 863 2123 212 44331 973 31 97 212 4433 23 31 32 54 75 86 97 212 443数据量:10 条排序耗时:3 毫秒前5个元素: 3, 23, 31, 32, 54后5个元素: 75, 86, 97, 212, 443快速排序
也是采用递归的思想,选取第一个或者任意一个元素为基准,以当前排序序列最左边为Left,最右边为Right,先让Right与基准元素大小,如果大则Right继续左移,如果小于或等于则停下来,再以同样方式让Left右移,如果大于或等于则停下来,当Left比Right小时则交换元素,直到Left和Right相遇停下来,此时i指向的是上一次作为基准元素的下标,这个序列的这个元素(i指向元素)左边所有元素一定比这个元素小,右边所有元素一定比这个元素大,以这个下标为分隔点,不包括这个元素,分割为两个待排序的子序列,继续递归排序,直到Left和Right指向同一元素。
private static void QuickSort(int[] arr, int left, int right) { if (left >= right) return;
// 选择中间元素作为基准,并交换到左端(挖坑法需要从端点开始) int mid = left + (right - left) / 2; Swap(ref arr[left], ref arr[mid]); // 将基准移到左端 int pivot = arr[left];
// 执行挖坑法分区 int partitionIndex = HolePartition(arr, left, right, pivot);
// 递归处理子数组 QuickSort(arr, left, partitionIndex - 1); QuickSort(arr, partitionIndex + 1, right); }
// 挖坑法分区方法 private static int HolePartition(int[] arr, int left, int right, int pivot) { int hole = left; // 初始坑位在左端
while (left < right) { // 右侧找小:从右向左找第一个小于基准的元素 while (left < right && arr[right] >= pivot) { right--; } arr[hole] = arr[right]; // 填坑 hole = right; // 新坑位
// 左侧找大:从左向右找第一个大于基准的元素 while (left < right && arr[left] <= pivot) { left++; } arr[hole] = arr[left]; // 填坑 hole = left; // 新坑位 }
arr[hole] = pivot; // 基准填入最后坑位 return hole; } #endregion堆排序
堆排序是建立在堆数据结构之上的。堆是一种完全二叉树,分为大根堆和小根堆,树的每一层都大于等于或者小于等于下一层,层内之间没有大小的排序。通常堆的第一个元素取顺序表下标为1的位置,层序构建初始的完全二叉树。
堆排序可以简单分为两个过程,首先是构建堆结构。使用递归的方式,从最后一个非叶子右节点开始,逐步向前构建一个大根堆,直到根节点结束,此时交换根节点和最后一个叶子节点位置,再把最后一个叶子节点移除,倒数第一个数就算排序完成,循环往复,直到排序完成。
//堆排序 #region 堆排序 public static void HeapSort(int[] arr) { Console.WriteLine("堆排序"); // 构建初始大顶堆 for (int i = arr.Length / 2 - 1; i >= 0; i--) { Heapify(arr, arr.Length, i); }
// 依次提取最大元素到数组末尾 for (int i = arr.Length - 1; i > 0; i--) { Swap(ref arr[0], ref arr[i]); // 将堆顶元素移到末尾 Heapify(arr, i, 0); // 调整剩余元素的堆结构 } }
private static void Heapify(int[] arr, int heapSize, int rootIndex) { int largest = rootIndex; // 初始化最大元素为根节点 int leftChild = 2 * rootIndex + 1; int rightChild = 2 * rootIndex + 2;
// 左子节点存在且大于根节点 if (leftChild < heapSize && arr[leftChild] > arr[largest]) { largest = leftChild; }
// 右子节点存在且大于当前最大值 if (rightChild < heapSize && arr[rightChild] > arr[largest]) { largest = rightChild; }
// 如果最大值不是根节点,则交换并递归调整 if (largest != rootIndex) { Swap(ref arr[rootIndex], ref arr[largest]); Heapify(arr, heapSize, largest); } } #endregion基数排序
基数排序就是将待排序的数字序列按照从个位、十位、百位、千位的数字这样的顺序一遍一遍排,直到最高位的数字排序完。
#region 基数排序 public static void RadixSort(int[] arr) { Console.WriteLine("基数排序"); if (arr == null || arr.Length < 2) return;
// 获取最大值确定位数 int max = GetMaxValue(arr);
// 从低位到高位进行排序 for (int exp = 1; max / exp > 0; exp *= 10) { CountingSortByDigit(arr, exp); } }
private static int GetMaxValue(int[] arr) { int max = arr[0]; for (int i = 1; i < arr.Length; i++) { if (arr[i] > max) max = arr[i]; } return max; }
private static void CountingSortByDigit(int[] arr, int exp) { int[] output = new int[arr.Length]; int[] count = new int[10];
// 统计当前位数字出现次数 for (int i = 0; i < arr.Length; i++) { count[(arr[i] / exp) % 10]++; }
// 计算累计位置 for (int i = 1; i < 10; i++) { count[i] += count[i - 1]; }
// 构建输出数组(逆序保证稳定性) for (int i = arr.Length - 1; i >= 0; i--) { int digit = (arr[i] / exp) % 10; output[count[digit] - 1] = arr[i]; count[digit]--; }
// 复制回原数组 Array.Copy(output, arr, arr.Length); } #endregion计数排序
计数排序就是先创建一个用于计算数量的序列,序列的起始和结束下标是待排序列的最小值和最大值,统计待排序列的元素出现个数,然后再输出。

#region 计数排序 public static void CountingSort(int[] arr) { Console.WriteLine("计数排序"); if (arr == null || arr.Length < 2) return;
// 获取数值范围 int min = arr[0], max = arr[0]; foreach (int num in arr) { if (num < min) min = num; if (num > max) max = num; }
// 创建计数数组 int[] count = new int[max - min + 1];
// 统计元素出现次数 foreach (int num in arr) { count[num - min]++; }
// 累加计数(计算最终位置) for (int i = 1; i < count.Length; i++) { count[i] += count[i - 1]; }
// 构建输出数组(反向遍历保证稳定性) int[] output = new int[arr.Length]; for (int i = arr.Length - 1; i >= 0; i--) { int index = arr[i] - min; output[count[index] - 1] = arr[i]; count[index]--; }
// 复制回原数组 Array.Copy(output, arr, arr.Length); } #endregion桶排序
桶排序思想很简单,就是对初始序列进行划分,划分出多个均匀的小区间,小区间内部使用任意算法进行排序。对于桶的划分可以有很多种,桶内排序也可以根据情况选择。

#region 桶排序public static void BucketSort(int[] arr){ Console.WriteLine("桶排序"); if (arr == null || arr.Length < 2) return;
// 1. 计算数值范围 int min = arr[0], max = arr[0]; foreach (int num in arr) { if (num < min) min = num; if (num > max) max = num; }
// 2. 动态计算桶参数(每个桶约1000范围) int bucketSize = 1000; int bucketCount = (max - min)/bucketSize + 1; List<List<int>> buckets = new List<List<int>>(bucketCount);
// 3. 初始化桶 for (int i = 0; i < bucketCount; i++) { buckets.Add(new List<int>()); }
// 4. 元素分配到桶 foreach (int num in arr) { int index = (num - min)/bucketSize; buckets[index].Add(num); }
// 5. 各桶使用插入排序(与现有代码风格统一) int indexArr = 0; foreach (var bucket in buckets) { if(bucket.Count == 0) continue;
// 调用现有的插入排序(需转换为数组) int[] temp = bucket.ToArray(); InsertionSort(temp);
Array.Copy(temp, 0, arr, indexArr, temp.Length); indexArr += temp.Length; }}#endregion部分信息可能已经过时



















